Differentiable Clustering

A step-by-step guide to Differentiable Clustering for Deep Learning.

Clustering

Clustering is one of the most classical and commonplace tasks in Machine Learning. The goal is to separate data $x_1, \ldots, x_n$ into $k$ groups, which are refered to as clusters. Clustering has wide-spread applications in bio-informatics, data compression, graphics, unsupervised and semi-supervised learning, as well as many other domains!

There is a large collection of well established clustering algorithms (with a select few being displayed in the table below).

Methodology	Examples	Possible Drawbacks
centroid	k-means	NP-Hard, heuristic (not direct solve of objective function).
connectivity	Linkage Algorithms (e.g. Single, UPGMA)	Computational Costly, Outliers.
distribution	EM Gaussian	Overfitting, Assumptions.

When dealing with semantic data e.g. Images or Text, applying such algorithms to the data directly is unlikely to lead to meaningful clusters. To see this, try applying k-means directly on the MNIST data set ! Instead, we would like to learn representations of are data e.g. features of a Neural Network, which when clustered, lead to clusters which capture meaningful semantic information.

Unfortunately, we cannot just plug any classical clustering algorithm into a Deep Learning pipeline Or more generally, gradient based learning pipeline. .

Why not? The answer is in the box below:

Gradient Based Learning Compatibility with Classical Clustering?

As a function, the solution of a clustering problem is piece-wise constant with respect to its inputs (such as a similarity or distance matrix), and its gradient would therefore be zero almost everywhere. This operation is therefore naturally ill-suited to the use of gradient-based approaches to minimize an objective, such as backpropagation for training Neural Networks.

If the above is not clear at first, just not that the cluster assignment of $x_i$ will almost always be the same as the cluster assignment for $x_i + \epsilon$ where $\epsilon$ denotes an infinitesimal change, so the gradient will be zero.

Goal

In this blog post we will give a simple explanation of our recent work that aims to address the above problem. We will keep math and other technical details to an absolute minimum, but for a more complete picture you can refer to the paper .

For any further questions, please feel free to contact me !

Kruskal’s Algorithm

Viewing our data as a graph

Firstly, we will recap maximum weight spanning forests and kruskals algorithm.

We can think of our data $x_1, \ldots, x_n \in \mathbb{R}^d$ as nodes of a fully-connected graph $K_n$, where the weight of an edge $(i,j)$ is given by the $(i,j)^{th}$ entry of a user-chosen similarity matrix $\Sigma \in \mathbb{R}^{n\times n}$. A large value of $\Sigma_{i,j}$ means that points $i$ and $j$ are similar, whilst a smaller value means that the points are disimilar.

Below is an example graph for two different typical choices of $\Sigma$.

Code for Figure

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
np.random.seed(123)

# Generate random nodes
N = 8
nodes = np.random.uniform(-1, 1, size=(N, 2))
fig, ax = plt.subplots(1, 2, figsize=(10, 4))

# Calculate pairwise distances
distances = -np.sum((nodes[:, np.newaxis] - nodes) ** 2, axis=-1)

cmap = plt.cm.get_cmap('plasma')
# Create a graph with nodes and edges
G = nx.Graph()
G.add_nodes_from(range(N))
for i in range(N):
    for j in range(i + 1, N):
        G.add_edge(i, j, weight=distances[i, j])

# Extract edge weights
edge_weights = [d['weight'] for u, v, d in G.edges(data=True)]
exp_edge_weights = [np.exp(e) for e in edge_weights]

# Create a graph plot
pos = dict(enumerate(nodes))  # Use the node positions as given by their coordinates
nx.draw(G, pos, node_size=100, node_color='black', ax=ax[0])
nx.draw(G, pos, node_size=100, node_color='black', ax=ax[1])

# Draw edges with colors based on weights
edges = nx.draw_networkx_edges(G, pos, edge_color=edge_weights, edge_cmap=cmap, edge_vmin=min(edge_weights), edge_vmax=max(edge_weights), width=2, ax=ax[0])

exp_edges = nx.draw_networkx_edges(G, pos, edge_color=exp_edge_weights, edge_cmap=cmap, edge_vmin=min(exp_edge_weights), edge_vmax=max(exp_edge_weights), width=2, ax=ax[1])

ax[0].set_xlim(-1, 1)
ax[0].set_ylim(-1, 1)

ax[1].set_xlim(-1, 1)
ax[1].set_ylim(-1, 1)

ax[0].set_title(r'$\Sigma_{ij} = - |\|x_i - x_j|\|_2^2$')
ax[1].set_title(r'$\Sigma_{ij} = \exp\left( - |\|x_i - x_j|\|_2^2\right)$')


plt.colorbar(edges, ax=ax[0])
plt.colorbar(exp_edges, ax=ax[1])
plt.tight_layout(pad=2.0)

plt.savefig('Kn.pdf')
plt.show()

Spanning trees

For the complete graph $K_n$ over nodes $\{x_1, \ldots, x_n\}$, we denote by $\mathcal{T}_n$ the set of spanning trees on $K_n$, i.e., subgraphs with no cycles and one connected component. Among these trees will be one or more that has maximum weight (the total weight of all edges in the tree), which is known as the maximum weight spanning tree.

Kruskals algorithm is a greedy algorithm to find a maximum weight spanning tree. It is incredibly simple, and consists of adding edges in a greedy manner to build the tree, and ignoring an edge if it would lead to a cycle. The psuedo-code for the algorithm is as follows:

# 
tree = {} 
edges = sort(edges)
for e in edges:
  if union(tree, {e}) has no cycle:
    tree = union(tree, {e})
  else:
    pass
  if tree is spanning:
    break

At each time step $t$, we will have a forest with $k=n-t$ connected components, where $n$ is the number of data points / nodes in the graph. A visual depiction of the algorithm in action can be seen below:

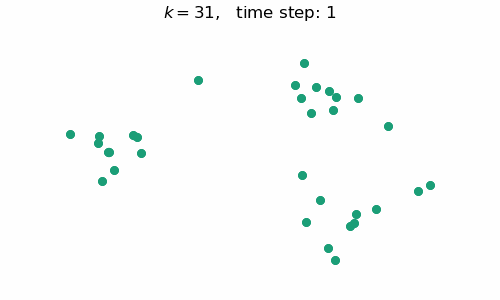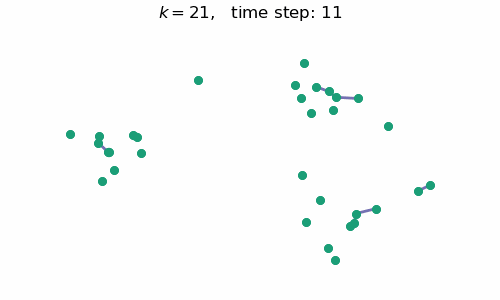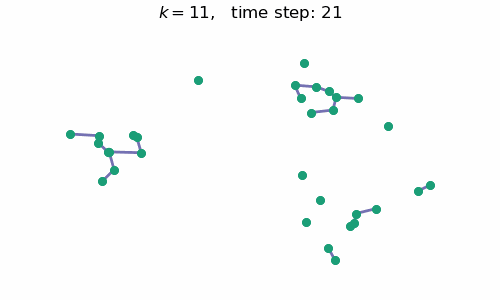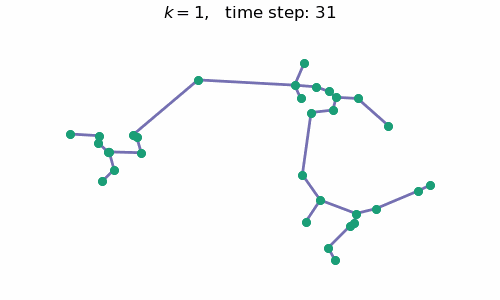
Code

import jaxclust
import jax
import jax.numpy as jnp
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from matplotlib.animation import FuncAnimation, PillowWriter
np.random.seed(0)


@jax.jit
def pairwise_square_distance(X):
    """
    euclidean pairwise square distance between data points
    """
    n = X.shape[0]
    G = jnp.dot(X, X.T)
    g = jnp.diag(G).reshape(n, 1)
    o = jnp.ones_like(g)
    return jnp.dot(g, o.T) + jnp.dot(o, g.T) - 2 * G

NODE_COLOR='#1b9e77'
EDGE_COLOR='#7570b3'
solver = jax.jit(jaxclust.solvers.get_flp_solver(False))

N_SAMPLES=32
X, Y, centers = make_blobs(n_samples=N_SAMPLES, centers=3, cluster_std=0.6, return_centers=True)

ids = np.argsort(Y)
X = X[ids]
Y = Y[ids]

S = - pairwise_square_distance(X)


writer = PillowWriter(fps=10, metadata=dict(artist='Me'), bitrate=1800)

fig, ax = plt.subplots(layout='constrained', figsize=(5, 3))
node_positions = {i: (X[i, 0], X[i, 1]) for i in range(N_SAMPLES)}
G = nx.Graph()
G.add_nodes_from(node_positions)

ax.set_ylim(X[:, 1].min() - 1, X[:, 1].max() + 1)
ax.set_xlim(X[:, 0].min() - 1, X[:, 0].max() + 1)

nx.draw(G, pos=node_positions, with_labels=False, node_size=32, node_color=NODE_COLOR, edge_color=EDGE_COLOR, ax=ax, width=2.0)

# Function to update the animation
def update_forest(step):
    if step != -1:
        ax.clear()

        A, M = solver(S, ncc=step)
        G = nx.Graph()

        node_positions = {i: (X[i, 0], X[i, 1]) for i in range(N_SAMPLES)}
        G.add_nodes_from(node_positions)

        edges = [(i, j) for i in range(N_SAMPLES) for j in range(i + 1, N_SAMPLES) if A[i, j] == 1]
        G.add_edges_from(edges)

        nx.draw(G, pos=node_positions, with_labels=False, node_size=32, node_color=NODE_COLOR, edge_color=EDGE_COLOR, ax=ax, width=2.0)
        ax.set_ylim(X[:, 1].min() - 1, X[:, 1].max() + 1)
        ax.set_xlim(X[:, 0].min() - 1, X[:, 0].max() + 1)
        ax.set_title(rf"$k = {step}$,   time step: {N_SAMPLES - step}")




frames = list(reversed(range(1, N_SAMPLES)))
frames = frames + [-1] * 30
animation = FuncAnimation(fig, update_forest, frames=frames, repeat=True, interval=100, repeat_delay=20000)

animation.save('mst.gif', writer=writer)
plt.show()

Obtaining Spanning Forests (early stopping)

When running Kruskal’s algorithm, one typically builds the tree $T$ by keeping track of the adjacency matrix $A\in \{0, 1\}^{n\times n}$ of the forest at each time step. We recall that:

\[\begin{equation*} A_{i,j} = 1 \Longleftrightarrow (i,j)\in T \end{equation*}\]

If we are to stop Kruskal’s algorithm one step before completion, we will obtain a forest with $k=2$ connected components. We can view these two connected components as clusters!

More generally, if we are stop the algorithm $k+1$ steps before completion, we will obtain a forest with $k$ connected components. Whats nice, is it turns out that Kruskal’s algorithm has a Matroid Structure, when means that if we stop the algorithm when the forest has $k$ connected components, that forest will indeed have maximum weight amongst all forests of $K_n$ that have $k$ connected components! More details are given in the box below, but they are not neccessary to understand the goal of this blog.

Optimality of Kruskal’s

The greedy optimality of Kruskal’s follows from the fact that the forests of $\mathcal{G}$ correspond to independent sets of the Graphic Matroid.

To verify this is true, note that the intersection of two forests is always a forest, and the spanning trees of a graph form the basis for the matroid. The matroid circuits can are the cycles in the graph. Optimality of Kruskal’s follows trivially (as the algorithm is equivalent to finding the maximum weight basis of the graph matroid).

From Adjacency Matrices to Cluster Information

We will now relate the process of construct a $k$-spanning forest to clustering.

Let $\mathcal{A}$ denote the set of all adjacency matrices corresponding to forests of $K_n$:

\[\begin{equation} \mathcal{A}=\{ A \subset \{0,1\}^{n\times n} : A \text{ is a forest of } K_n\}, \end{equation}\]

and let $\mathcal{A}_k \subset \mathcal{A}$ denote such adjacency matrices that have $k$ connected components. To relate an adjacency matrix $A\in \mathcal{A}$ to clustering, we define the cluster equivalence function:

\[\begin{equation} M : \mathcal{A} \rightarrow \{0,1\}^{n \times n} \end{equation}\] \[M(A)_{i,j} = \begin{cases} 1 \quad &\text{if} \quad (i, j) \text{ are in the same connected component.} \\ 0 \quad &\text{if} \quad (i, j) \text{ are in different connected components.} \\ \end{cases}\]

One can view the connected components of a forest as clusters, with two points $x_i$ and $x_j$ being in the same cluster if and only if $M(A)_{ij} = 1$. For short hand, when talking about a fixed $A_k\in \mathcal{A}_k$, we write $M_k := M(A_k)$.

Relationship between $A_k$ and $M_k$

You might have noticed that two different adjacency matrices (i.e. members of $\mathcal{A}_k$) may correspond to the same $M_k$. Indeed, relabelling points from the same connected component changes $A_k$, but will leave the corresponding $M_k$ unchanged.

Clearly the cluster equivalence mapping $M$ is not injective. It turns out that $M$ is an equivalence relation, and the equivalence classes of $M$ are the sets of adjacency matricies mapping to the same cluster equivalence matrix (hence the equivalence being features in its name)!

Clustering with Spanning Forests (aka Single Linkage)

We can hence obtain a clustering by running Kruskal’s to construct the maximum weight $k$-spanning forest:

def cluster(Sigma, k)
  do:
    run kruskals step until k connected components
  return: A_k, M_k

This algorithm is known as Single-Linkage and is related to a family of hierarchical clustering algorithms. An example of the algorithm running is given below, where the data is separated into three distinct clusters:

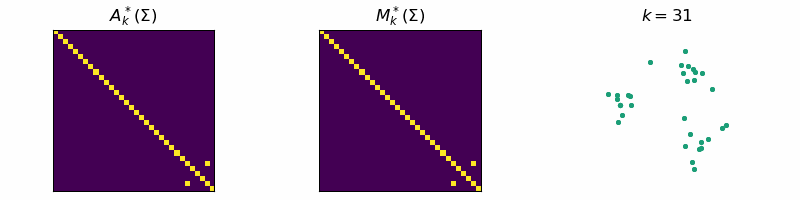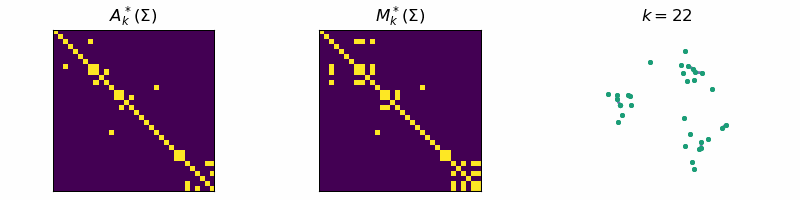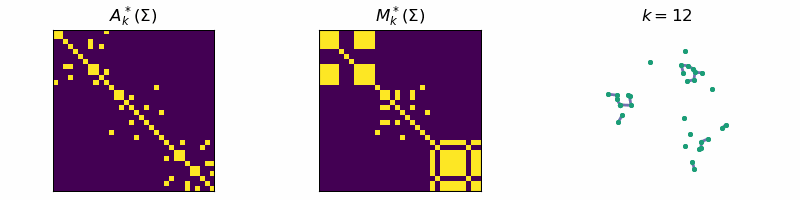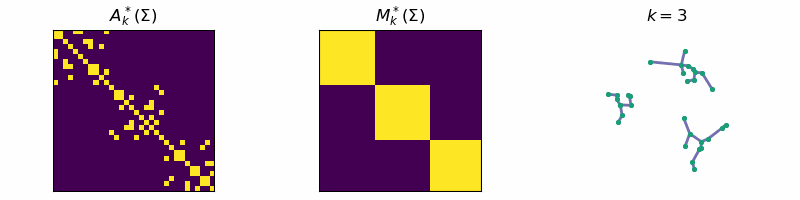
Code

  fig, ax = plt.subplots(1, 3, layout='constrained', figsize=(8, 2))
  node_positions = {i: (X[i, 0], X[i, 1]) for i in range(N_SAMPLES)}
  G = nx.Graph()
  G.add_nodes_from(node_positions)

  ax[2].set_ylim(X[:, 1].min() - 0.1, X[:, 1].max() + 0.1)
  ax[2].set_xlim(X[:, 0].min() - 0.1, X[:, 0].max() + .1)

  nx.draw(G, pos=node_positions, with_labels=False, node_size=8, node_color=NODE_COLOR, width=2.0, ax=ax[2], edge_color=EDGE_COLOR)
  ax[2].set_title('k = 64')
  ax[0].set_title(r'$A_{k}^*(\Sigma)$')
  ax[1].set_title(r'$M_{k}^*(\Sigma)$')
  ax[0].imshow(np.eye(N_SAMPLES))
  ax[1].imshow(np.eye(N_SAMPLES))

  ax[0].set_xticks([])
  ax[0].set_yticks([])

  ax[1].set_xticks([])
  ax[1].set_yticks([])
  ax[2].set_aspect('equal', adjustable='box')

# Function to update the animation
def update_cluster(step):
    if step!=-1:
        ax[0].clear()
        ax[1].clear()
        ax[2].clear()

        A, M = solver(S, ncc=step)

        G = nx.Graph()

        node_positions = {i: (X[i, 0], X[i, 1]) for i in range(N_SAMPLES)}
        G.add_nodes_from(node_positions)

        # Identify edges based on the adjacency matrix
        edges = [(i, j) for i in range(N_SAMPLES) for j in range(i + 1, N_SAMPLES) if A[i, j] == 1]
        G.add_edges_from(edges)

        # Draw the graph
        nx.draw(G, pos=node_positions, with_labels=False, node_size=8, node_color=NODE_COLOR, width=2, ax=ax[2], edge_color=EDGE_COLOR)


        ax[2].set_ylim(X[:, 1].min() - 1, X[:, 1].max() + 1)
        ax[2].set_xlim(X[:, 0].min() - 1, X[:, 0].max() + 1)

        ax[0].imshow(A)
        ax[0].set_title(r'$A_{k}^*(\Sigma)$')
        ax[0].set_xticks([])
        ax[0].set_yticks([])
        ax[1].imshow(M)
        ax[1].set_title(r'$M_{k}^*(\Sigma)$')
        ax[1].set_xticks([])
        ax[1].set_yticks([])
        ax[2].set_title(fr"$k = {step}$")

        ax[2].set_aspect('equal', adjustable='box')


frames = list(reversed(range(3, N_SAMPLES)))
frames = frames + [-1] * 50
animation = FuncAnimation(fig, update_cluster, frames=frames, repeat=True, interval=25, repeat_delay=2500)
animation.save('kruskals.gif', writer=writer)
plt.show()

In this section we have explored how one can perform a clustering by building spanning forests using Kruskal’s algorithm (Singe Linkage). But how does this get us close to differentiable clustering? To answer this question we need to look at perturbations!

Perturbations of LPs

We will now take a pause from Kruskal’s algorithm to look at perturbations, sometimes also called randomized smoothing. If maths isn’t your thing, not to worry as understanding the perturbations / smoothing in detail is not neccessary for getting a grasp of the overall methodology. For further reading and a more depth exploration of the subject, I would certainly recommend checking out Francis Bach’s blogpost on the subject!

For a convex hull $\mathcal{C} \subset \mathbb{R}^d$ we define:

argmax solution $y^*:\mathbb{R}^d \rightarrow \mathbb{R}^d$
max solution $F:\mathbb{R}^d\rightarrow\mathbb{R}$

as follows:

\[\DeclareMathOperator{\argmax}{argmax} \begin{align} y^*(\theta) &= \underset{y \in \mathcal{C}}{\argmax} \langle y, \theta \rangle. \\[1em] F(\theta) &= \max\limits_{y \in \mathcal{C}} \langle y, \theta \rangle. \end{align}\]

We begin by remarking that for any $\theta \in \mathbb{R}^d$, $y^*(\theta)$ will always be one of the extreme points of the convex hull This follows from the linearity of the inner-product combined with the definition of a convex hull. . For this reason both $y^*$ and $F$ are piece-wise constant in $\theta$.

Hence the gradient $\nabla_\theta F(\theta) \in \mathbb{R}^d$ and Jacobian $J_\theta y^*(\theta)\in \mathbb{R}^{d\times d}$ will be zero almost everywhere, similar to the case of classical clustering algorithms.

To get differentiability, we would like that as $\theta$ changes, $y^*(\theta)$ moves smoothly along the convex hull, instead of jumping from extreme point to extreme point. To do this we will induce a probability distribution by replacing $\theta$ in the above, by $\theta + \epsilon Z$, where $Z$ is some an exponential-family random variable e.g. multi-variate Gaussian with zero mean and identity covariance. This induces a probability distribution:

\[\mathbb{P}_Y(Y = y ; \theta) = \mathbb{P}_Z(y^*(\theta + \epsilon Z) = y)\]

How can we understand this? Firsly lets fix $\theta$ and the noise amplitude $\epsilon > 0$. Provided the noise amplitude is large enough, the argmax solution $y^*_\epsilon(\theta + \epsilon Z )$ is now a random variable, taking each of the extreme values of the convex hull with a given probability. By taking the expected value, we can obtain a smoothing!

This yields the perturbed versions of both the argmax and the max:

\[\DeclareMathOperator{\argmax}{argmax} \begin{align} y^*_\epsilon(\theta) &= \textcolor{orange}{\mathbb{E}_Z}\left[\underset{y \in \mathcal{C}}{\argmax} \langle y, \theta + \epsilon \textcolor{orange}{Z} \rangle\right]. \\[1em] F_\epsilon(\theta) &= \textcolor{orange}{\mathbb{E}_Z}\left[\max\limits_{y \in \mathcal{C}} \langle y, \theta + \epsilon \textcolor{orange}{Z} \rangle \right]. \end{align}\]

We note that as $\epsilon \rightarrow 0$, both $F_\epsilon(\theta) \rightarrow F(\theta)$ and $y^*_\epsilon(\theta) \rightarrow y^*(\theta)$. There are many other properties of the perturbed argmax and max (such as bounding their difference with their unperturbed counterparts), and for further reading we refer the reader to . The figure below depicts the smoothing, (thanks to Quentin Berthet for providing it):

Illustration of smoothing with perturbations.

Gradients of smoothed proxies

When the noise distribution is of exponential family, both the gradient of the perturbed max $\nabla_\theta F_\epsilon(\theta)$ and the Jacobian of the perturbed argmax $J_\theta y^*_\theta(\theta)$ can be expressed as both an expectation of a function of the max $F$ and as an expectation of a function of the argmax $y^*$. The details are expressed in the Lemma in the box below:

Gradients for Perturbed Proxies .

For noise distribution $Z$ with distribution having density $d\mu(z) = \exp(-\nu(z))dz$ with $\nu$ twice differentiable:

\[\begin{align*} \nabla_\theta F_\epsilon(\theta) &= \textcolor{orange}{\mathbb{E}_Z}\left[ y^*(\theta + \epsilon\textcolor{orange}{Z}))\right]\\ &= \textcolor{orange}{\mathbb{E}_Z}\left[ F(\theta + \epsilon \textcolor{orange}{Z})\textcolor{orange}{\nabla_z \nu(Z)} / \epsilon \right]. \\[1.5em] J_\theta y^*_\epsilon(\theta) &= \textcolor{orange}{\mathbb{E}_Z}\left[y^*(\theta + \epsilon \textcolor{orange}{Z})\textcolor{orange}{\nabla_z\nu(Z)^T} /\epsilon \right] \\ &= \textcolor{orange}{\mathbb{E}_Z}\left[F(\theta + \epsilon \textcolor{orange}{Z})(\textcolor{orange}{\nabla_z\nu(Z)\nabla_z\nu(Z)^T - \nabla_z^2\nu(Z)}) / \epsilon^2 \right]. \end{align*}\]

We note that if we can solve the LP efficiently, then both of these gradients can be calculated efficiently in parallel using Monte-Carlo sampling, and hence are suitable for accelerators such as GPUs and TPUs!

Perturbations for clustering

Lets connect the perturbed proxies we saw above to clustering!

It turns out that the maximum weight $k$-spanning forest can be in fact written in the LP form, where its adjacency matrix is expressed as an argmax and its total weight as a max. This makes it compatible for using the perturbations smoothing from the previous section!

To see this, let $\mathcal{C}_k = cvx(\mathcal{A}_k)$ be the convex hull of trees with $k$ connected components. Then the adjacency matrix of the maximum weight $k$-spanning forest takes the form of an argmax:

\[\begin{equation} A_k^*(\Sigma) = \underset{A\in \mathcal{C}_k}{\argmax}\left\langle A, \Sigma \right\rangle. \end{equation}\]

Its corresponding total weight, take the form of a max:

\[\begin{equation} F_k(\Sigma) = \max_{A\in \mathcal{C}_k}\left\langle A, \Sigma \right\rangle. \end{equation}\]

Hence applying perturbations to this LP we can obtain differentiable proxies:

\[\DeclareMathOperator{\argmax}{argmax} \begin{align} A^*_{k,\epsilon}(\Sigma) &= \textcolor{orange}{\mathbb{E}_Z}\left[\underset{A \in \mathcal{C}_k}{\argmax} \langle A, \Sigma + \epsilon \textcolor{orange}{Z} \rangle\right]. \\[1em] F_{k,\epsilon}(\theta) &= \textcolor{orange}{\mathbb{E}_Z}\left[\max\limits_{A \in \mathcal{C}_k} \langle A, \Sigma + \epsilon \textcolor{orange}{Z} \rangle \right]. \end{align}\]

The animation below depicts how $A^*_{k, \epsilon}$ and $M^*_{k, \epsilon}$ change for varied $\epsilon > 0$ in the case of $k=3$.

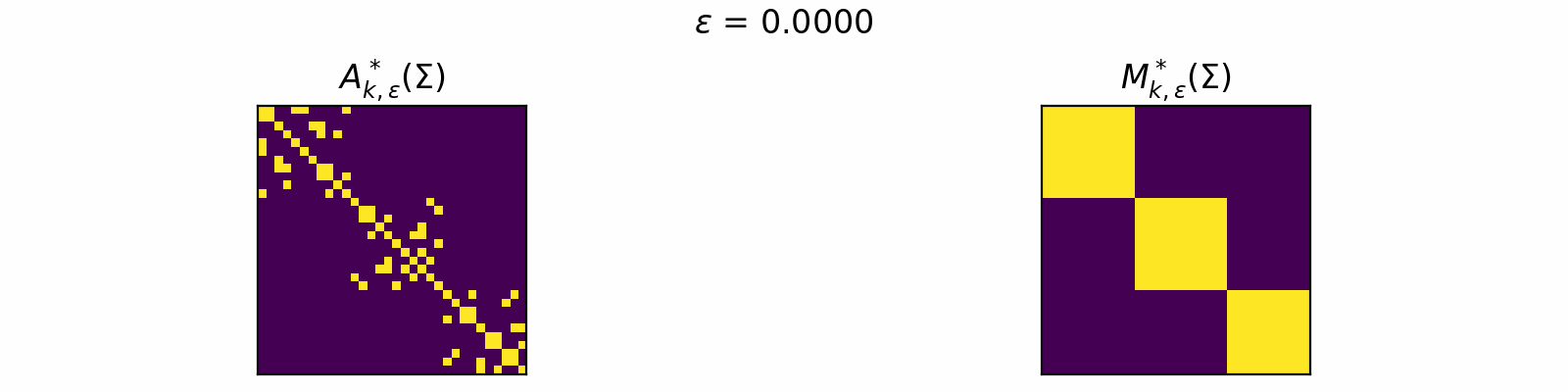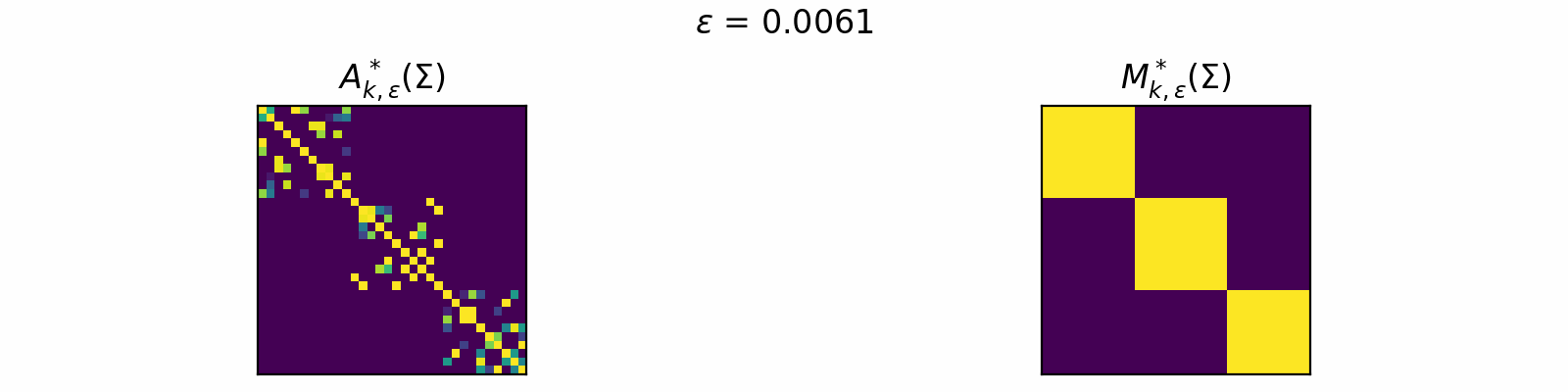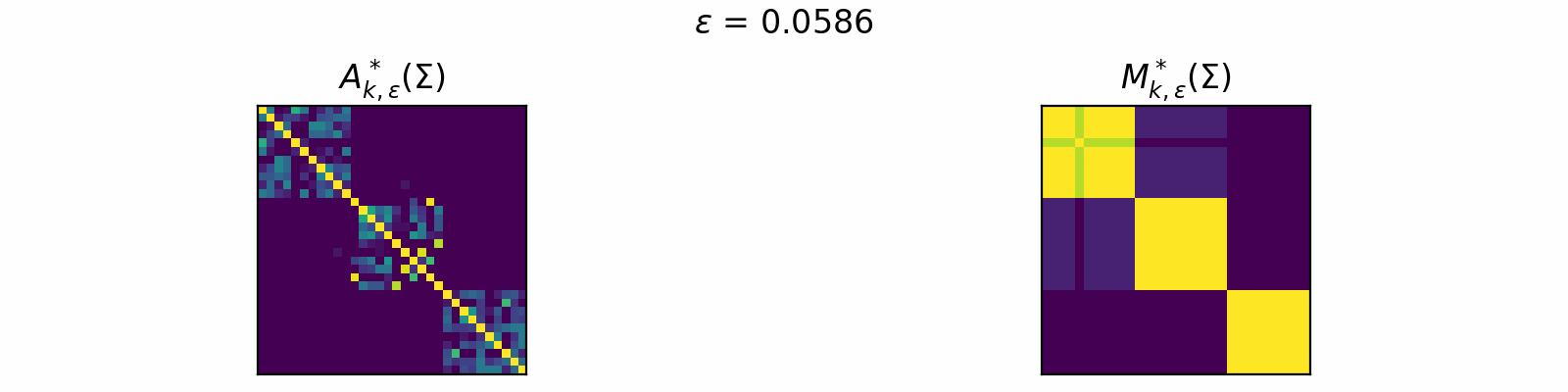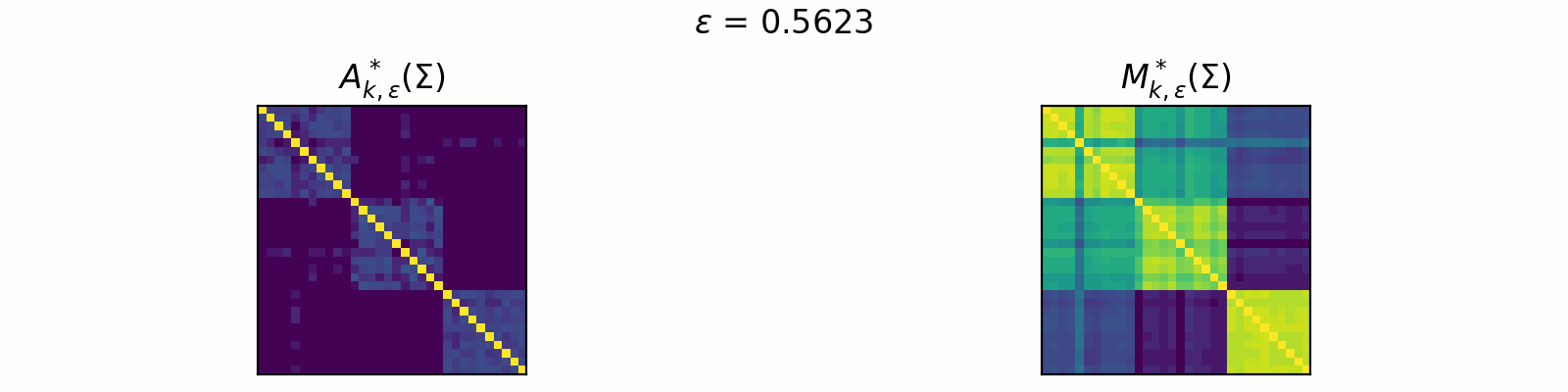
Code

import jaxclust
import jax
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from matplotlib.animation import FuncAnimation, PillowWriter
np.random.seed(0)

@jax.jit
def pairwise_square_distance(X):
    """
    euclidean pairwise square distance between data points
    """
    n = X.shape[0]
    G = jnp.dot(X, X.T)
    g = jnp.diag(G).reshape(n, 1)
    o = jnp.ones_like(g)
    return jnp.dot(g, o.T) + jnp.dot(o, g.T) - 2 * G

solver = jax.jit(jaxclust.solvers.get_flp_solver(False))
pert_solver = jax.jit(jaxclust.perturbations.make_pert_flp_solver(solver, constrained=False))

N_SAMPLES=32
X, Y, centers = make_blobs(n_samples=N_SAMPLES, centers=3, cluster_std=0.6, return_centers=True)

ids = np.argsort(Y)
X = X[ids]
Y = Y[ids]

S = - pairwise_square_distance(X)
S = (S - S.mean()) / S.std()

writer = PillowWriter(fps=10, metadata=dict(artist='Me'), bitrate=1800)
fig, ax = plt.subplots(1, 2, layout='constrained', figsize=(8, 2))
plt.suptitle(rf'$\epsilon$ = {0:.4f}')


ax[0].set_title(r'$A_{k}^*(\Sigma)$')
ax[1].set_title(r'$M_{k}^*(\Sigma)$')

A_, M_ = solver(S, 3)

ax[0].imshow(A_)
ax[1].imshow(M_)
ax[0].set_xticks([])
ax[0].set_yticks([])
ax[1].set_xticks([])
ax[1].set_yticks([])

# Function to update the animation
def update_cluster(epsilon):
    ax[0].clear()
    ax[1].clear()
    if epsilon == 0:
        A, M = A_, M_
    else:
        A, F, M = pert_solver(S, ncc=3, sigma=epsilon, rng=jax.random.PRNGKey(0))

    ax[0].imshow(A)
    ax[0].set_title(r'$A_{k, \epsilon}^*(\Sigma)$')
    ax[0].set_xticks([])
    ax[0].set_yticks([])
    ax[1].imshow(M)
    ax[1].set_title(r'$M_{k, \epsilon}^*(\Sigma)$')
    ax[1].set_xticks([])
    ax[1].set_yticks([])
    plt.suptitle(rf'$\epsilon$ = {epsilon:.4f}')


frames = 10 **  np.linspace(-3, -0.25, 15)
frames = jnp.concatenate((jnp.zeros(10), frames, jnp.ones(10) * frames[-1]))

animation = FuncAnimation(fig, update_cluster, frames=frames, repeat=True, interval=25, repeat_delay=2500)
animation.save('pertkruskals.gif', writer=writer)
plt.show()

So at this point we have a clustering method which:

Is differentiable!
Whose gradients can be computed as a Monte Carlo estimator in parallel.
Compatible with accelerators and autodiff (since all operatiors are matmal).

Lets look at one potential application (among many).

Incorporating Partial Information

Suppose we have data where some (or all) of the points have labels i.e. a semi-supervised learning or fully-supervised learning setting. We would ideally like to learn representations of our data, which when clustered, respect this label information.

To illustrate this point, lets consider the simple example below, where the embeddings of a batch of data are depicted by the circles. Lets suppose that the two red points share the same label e.g. cat which is different from that of the blue point e.g. dog, whilst all other points are unlabelled.

Partial label Information can be encoded via must links and must-not links.

If we were to cluster these embeddings into two clusters, using our approach described above, we would obtain something like the depiction below:

test

However, this is clustering is inconsistent with the label information, since the blue point is now in the same cluster as the two red points.

To enforce label consistency, we can encode all the label information into a $n\times n$ constraint matrix $M_\Omega$ (depicted above), whose $(i, j)^{th}$ entry is:

$1$ if both $i$ and $j$ should be in the same connected component i.e. a must-link constraint.
$0$ if $i$ and $j$ should not be in the same connencted component i.e. a must-not link constraint.
$\star$, a special value signifing there are no constraints between $i$ and $j$.

Note the must-link and must-not-link constraints are very general concepts, and go beyond label information. For example, such constraints can ecompass active learning, self-supervised learning and fairness conditions.

For any constraint matrix $M_\Omega$, we can also consider modified versions of the maximum weight $k$-spanning forest LP, restricted to the set of forests that respect the constraint matrix $\mathcal{C}_k(M_\Omega)$:

\[\begin{equation} A_k^*(\Sigma ; M_\Omega) = \underset{A\in \mathcal{C}_k(M_\Omega)}{\argmax}\left\langle A, \Sigma \right\rangle. \end{equation}\] \[\begin{equation} F_k(\Sigma ; M_\Omega) = \max_{A\in \mathcal{C}_k(M_\Omega)}\left\langle A, \Sigma \right\rangle. \end{equation}\]

Unfortunately, the above LP has a matroid structure only in certain settings, so running Kruskal’s algorithm but adding checks for must-not-link constraints and enforcing must-link constraints will not guarentee optimality. It is however, a suitable heurestic that we can still use to obtain clusters satisfying our constraint matrix $M_\Omega$. For details on how to implement the constained clustering, see the source code of JaxClust.

Solving the LP with constrained clustering would result in the clusters displayed below:

test

A Loss Function for Differentiable Clustering

Since $\mathcal{C}_k(M_\Omega) \subseteq \mathcal{C}$, it trivially follows that $F_k(\Sigma ; M_\Omega) \leq F_k(\Sigma )$. In words, the total weight of the maximum $k$-spanning forest will always be greater than or equal to the total weight of the maximum $k$-spanning forest satisfying the constraint matrix $M_\Omega$, simply as there are more forests to choose from!

We can design a loss function:

\[\ell(\Sigma ; M_\Omega) = F_k(\Sigma) - F_k(\Sigma ; M_\Omega).\]

The above loss function is non-negative, and is zero if and only if the clustering with the constraint matrix $M_\Omega$ leads to a forest having the same weight as with no constraints. We can think of this as “the loss will be zero if the embeddings are in a position that satisfies the label constraints”.

Furhermore, by replacing $F_k$ with $F_{k, \epsilon}$, this loss function can be smoothed as we have previously seen:

\[\ell_\epsilon(\Sigma ; M_\Omega) = F_{k,\epsilon}(\Sigma) - F_{k, \epsilon}(\Sigma ; M_\Omega).\]

We remark that the gradient of the loss function can be trivially calculated as:

\[\nabla_\Sigma \ell_\epsilon(\Sigma ; M_\Omega) = A_{k,\epsilon}(\Sigma) - A_{k, \epsilon}(\Sigma ; M_\Omega).\]

Hence the gradient the $\ell_\epsilon$ corresponds to the difference of the adjacency matrix of the constrained and unconstrained spanning forest.

We refer to this loss as the Partial-Fenchel Young loss, which turns out to have many desirable statistical properties. The loss can also be expressed as an infinium loss (a.k.a partial loss) over a Fenchel-Young objective , hence its nomenclature. For more information on the properties and forms of this loss, please refer to the paper .

Semi-Supervised Learning Pipeline

An example pipeline to learn embeddings from partial information is depicted below.

Embeddings $V$ are generated from data $X$ using a model (e.g. a neural network), parameterized by weights $w$. From these embeddings one can construct a similarity matrix $\Sigma$ and calculate the Partial FY loss using any label constraints available for the batch. The model weights are updated in the backwards pass, informed by the gradients previously discussed above.

This methodology can lead to embeddings that are clusterable, and suitable for down-stream transfer learning via a linear probe. For experiments using this pipeline, please refer to our paper!

Class Discovery

It turns out our clustering methodology allows a neural network to learn meaningful representations from partial label information even in the difficult situation where some classes are unaccounted for.

Below is a tSNE visualization of embeddings for a small CNN (LeNET) trained on the MNIST data set with all but 100 labels have been withheld, and where three of the ten classes have no labels present in the train set (depicted in bold).

Despite never seeing a label for these three classes, the model has leveraged partial label information through clustering to infer these classes. Investigating potential applications of learning through clustering to zero-shot and self-supervised learning are promising avenues for future work.